#5. 지도학습에서의 과적합화
1. Intro
분류와 회귀
분류는 두 개의 계층(클래스)으로만 분류하는 이진binary 분류와 셋 이상의 계층으로 분류하는 다중multiclass 분류로 구분된다.
회귀는 연속적인 숫자(부동소수점수 또는 실수)를 예측하는 것이다. 예측값은 범위 내의 어떤 숫자든 가능하다.
분류와 회귀는 예측값의 연속성 성질에 따라 구분할 수 있다. 전자는 비연속적인 반면, 후자는 연속적인 값을 가진다.
일반화, 과적합
모델이 처음 보는 데이터를 정확하게 예측하면 일반화가 되었다고 말할 수 있다.
훈련 데이터로 만든 모델이 시험 데이터의 레이블을 정확하게 예측하면, 모델이 일반화됐다고 말할 수 있는 것이다.
하지만 모델의 복잡도가 높아질수록 그 모델은 훈련 세트에 최적화된 모델이 되어버려 과적합을 야기할 수 있다.
2. 과적합화 문제에 대하여
일반화
- 일반화: 모델 제작에 사용되지 않은 모든 데이터에 대해 모델을 적용할 수 있는 성질
- 과적합화: 학습되지 않은 데이터에 대한 일반화가 안되고 훈련 데이터에만 모델을 최적화하려는 경향
우리는 지도 학습 모델을 만들 때 훈련 데이터에서 패턴을 찾아내야 한다. 그리고 그것을 일반화해야 한다.
해당 패턴으로 일반화 될 수도 있지만, 그것은 훈련 데이터셋에만 존재하는 우연한 패턴일 수도 있다.
이처럼 일반화되지 않고 훈련 데이터와 같이 조사한 데이터에만 존재하는 특성을 '데이터 과적합화'라고 부른다.
모든 데이터 마이닝 과정에는 과적합화의 위험이 존재한다. 모델이 복잡해질 수록 과적합화 경향이 커지기 때문이다.
과적합화 검사하기
- 적합도 그래프Fitting Graph: 복잡도에 따른 모델의 정확도를 보여주는 도구
- 예비 데이터Holdout Data: 시험 데이터의 다른 표현. 모델 평가시에는 훈련 데이터를 사용할 수 없기에 모델링 전에 따로 떼어둔 데이터셋.
모델 성능 측정을 위해 사용하는 데이터다. 예비 데이터의 타겟값은 공개되지 않으며, 모델이 예측한다. 그리고 예측값과 실제 타겟값을 비교해 일반화 성능을 추정한다.
모델의 정확도는 복잡도에 따라 달라진다. 그리고 복잡도가 높을수록 과적합화 문제가 심해진다.

그래프의 x축은 모델의 복잡도를 의미하고 y축은 오류율을 나타낸다.
그림에서 볼 수 있듯이, 모델의 복잡도에 따른 훈련 데이터와 시험(예비)데이터의 정확도는 서로 다른 양상으로 변화한다.
훈련 데이터에 대한 오류율은 모델의 복잡도가 증가함에 따라 지속적으로 감소하지만, 예비 데이터의 오류율은 어느순간 증가하기 시작한다.
예비 데이터와 훈련 데이터 사이의 정확도에 괴리가 생기면 일반화 특성이 감소하고 과적합과 되었다고 판단할 수 있다.
트리 유도에서의 과적합화
단말 노드 안에 데이터가 하나씩만 있다면 그 트리 모델은 과적합화되었다고 할 수 있다. 노드의 개수기 늘어날수록 복잡도가 커진다고 생각하면 된다.
그러나 과적합화된 트리 모델은 예비 데이터를 어떻게든 하나의 단말 노드(계층)에 도달하게 한다. 그래서 다른 과적합 모델보다 조금 낫다고 한다.
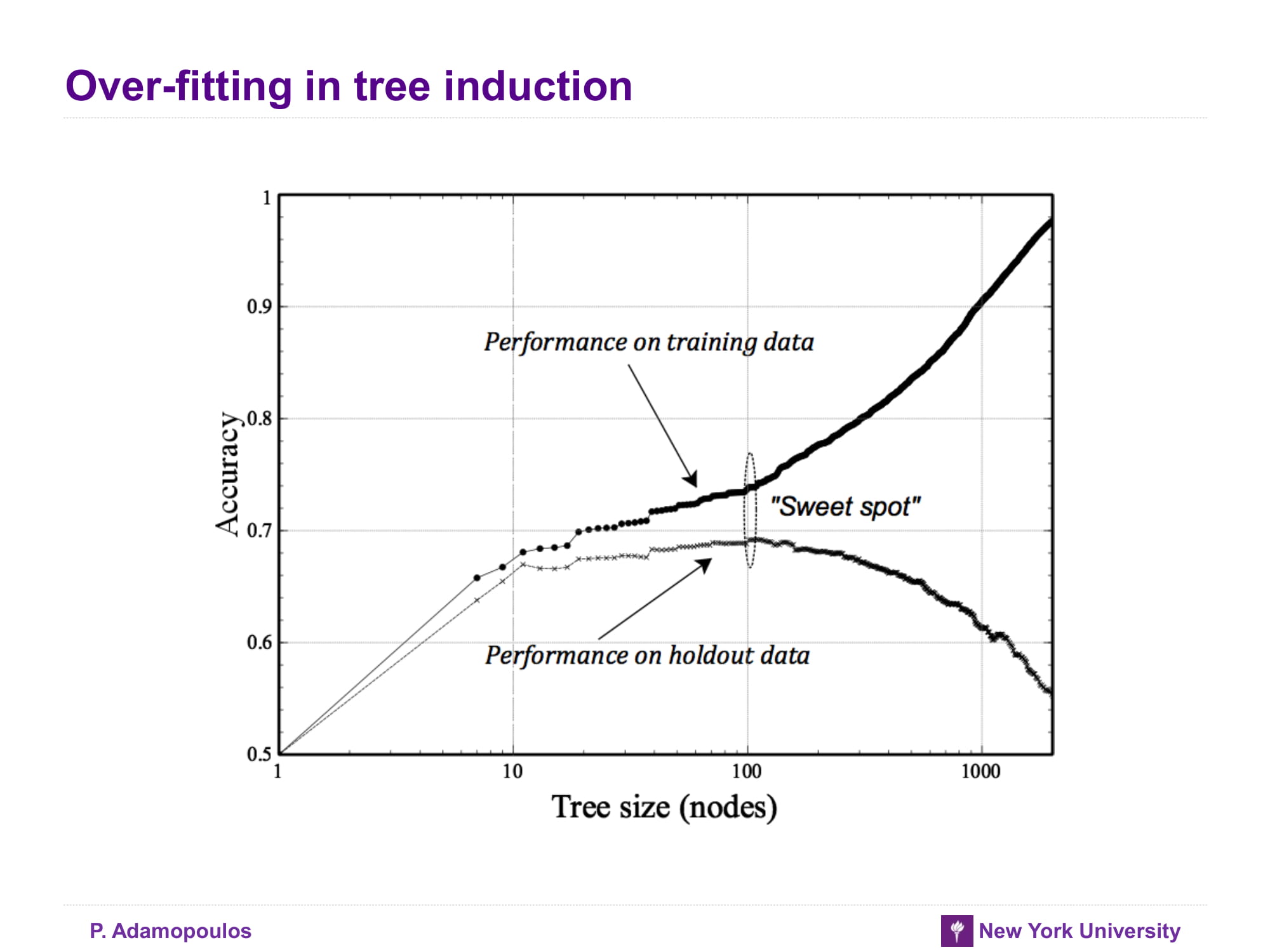
아래 그래프는 트리 유도에 대한 적합도 그래프이다. x축은 노드의 개수(복잡도의 척도), y축은 오류율을 나타낸다.
트리의 노드 개수마다 새로 훈련 데이터를 사용해 트리를 만들고, 각 상황마다의 훈련 데이터와 예비 데이터의 측정결과를 비교해 정확도를 측정한다.
트리의 크기가 작을 때는 노드의 개수가 늘어남에 따라 양 세트의 정확도가 올라간다. 훈련 세트의 정확도는 예비보다 조금 높다.
그러나 과적합화되는 순간부터 예비 데이터셋의 정확도는 급락하기 시작한다. 그리고 훈련 데이터셋에 대한 정확도는 계속 상승한다.
과적합이 되는 지점 즉 훈련 데이터와 예비 데이터의 정확도 괴리가 발생하기 시작하는 지점을 스위트 스팟이라고 한다.
과적합화를 막기 위해서는 early stopping을 통해 훈련 데이터의 학습을 중지시켜야 한다.
3. 과적합화와 수학
수학 함수에서 복잡도를 부여하는 방법은 아래 소개한 방법 외에도 여려가지가 있다.
속성 추가하기
2차원 객체 공간을 계층에 따라 분류하는 경계선을 선형 분류자라고 한다. 선형 분류자는 분류 함수로 표현할 수 있다.
이 식을 선형 판별식이라고 하며, 아래 식과 같이 속성들의 가중치의 합과 같다.
간단히 말하자면, 감독 세분화할때 객체들을 분류하는 기준을 아래 함수와 같이 속성들의 가중치 합으로 표현할 수 있다는 것이다.
$f(x) = w_0 + w_1x_1 + w_2x_2 + w_3x_3$
($x$는 속성, $w$는 파라미터(가중치)를 의미한다)
속성이 추가될수록 모델이 학습해야 하는 파라미터의 개수가 늘어나므로 함수는 복잡해진다.
속성$x_i$를 추가해 선형 함수의 복잡도를 높일 수 있지만, $x_4 = x_2^2$와 같은 비선형 속성을 추가해 선형 모델을 비션형 모델로 바꿀 수 있다.
어떻게 됐든간에 속성을 추가하면 모델은 복잡해진다. 훈련 세트에 대한 적합도가 올라간다는 의미이다.
'배우는 것 > Maching Learning' 카테고리의 다른 글
| #7. 파이썬 기본지식 공부(2)_스칼라형, 튜플, 리스트, 사전 (0) | 2021.12.23 |
|---|---|
| #6. 파이썬 기본지식 공부(1) (0) | 2021.12.21 |
| #4. 얼렁뚱땅 주피터로 맛보기학습 (0) | 2021.12.19 |
| #3. 분류 트리, 트리 구조 모델, 분할정복법, 논리문 (0) | 2021.12.19 |
| #2. 감독 학습, 정보를 전달하는 속성, 엔트로피, 정보증가량(IG) (0) | 2021.12.17 |














